

Find the angular displacement of the car wheel in the process.First, let us make some simplifications in notation. Question 7: The wheel of a racing car catches a speed of 40rad/s in 4 seconds. Find the angular displacement of the car wheel in the process.įor finding out the value of “a”, the first equation of motion can be used.įor finding out the distance, a third equation of motion will be used. Question 6: The wheel of a racing car catches a speed of 20rad/s in 2 seconds. If the initial speed was 10rad/s, what would be the angle covered in 10 seconds? Question 5: If a body is moving at an angular acceleration of 2 rad/s 2. If the initial speed was 40rad/s, what would be the angle covered in 3 seconds?įor finding out the value of “ “, the first equation of motion can be used. Question 4: If a body is moving at an angular acceleration of 5 rad/s 2. If the initial angular velocity was 30rad/s, what would be the speed in 5 seconds? Question 3: If a body is rotating with an acceleration of -10 radians/s 2. Let denote the initial angular velocity and denote the final angular velocity.įor finding out the value of “v”, the first equation of motion can be used. If the initial angular velocity was 15rad/s, what would be the speed in 5 seconds?
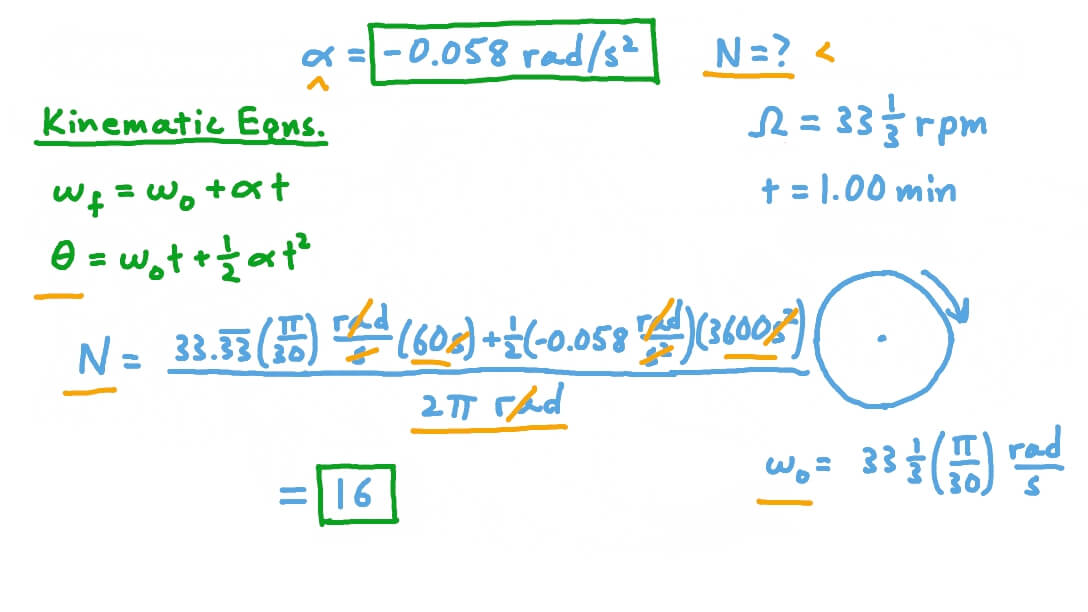
Question 2: If a body is rotating with an acceleration of 2 radians/s 2. Question 1: If a body is rotating at an angular velocity of 15rad/s, what would be the angular displacement in 5 seconds? Keep in mind that these equations are only for situations where angular acceleration is constant. The equations governing this motion are given below. Let’s say the time is denoted by “t”, present angular velocity by ω, initial velocity by, and the angle covered by the object by θ. Kinematic Equations for Rotational Motionįor an object rotating with an angular acceleration α. Displacement “s” is analogous to angle of rotation( θ), acceleration(a) is analogous to angular acceleration( α). Now, in the case of rotational motion, velocity(v) corresponds to the angular velocity( ω). Keep in mind that these equations are only for situations where acceleration “a” is constant and the object is moving in a straight line. Let’s say the time is denoted by “t”, present velocity by “v”, initial velocity by “u” and the distance covered by the object by “s”. Rotationalįor an object moving with an acceleration “a”.
The table below represents some analogous quantities. These equations are called kinematic equations of rotational motion. A similar approach can be used in rotational motion. These parameters can be calculated using the kinematics of linear motion. This situation is similar to a vehicle moving on a road with some acceleration and attaining some velocity. In terms of the formal notation, it can be said that a wheel having a large α ends up rotating at a large angle through a number of revolutions ( θ). Solution: The dynamic viscosity calculator provides the density and the viscosity of water at 20 c as follow: Dynamic viscosity 1.0016 mPa.s. Consider a wheel that starts spinning with angular acceleration and covers many revolutions. Let’s see how the equation of motion relates to the equations of rotational motion. Rotational quantities such as angle θ, angular velocity ω, and angular acceleration α. Average and Instantaneous Rate of Change.Class 11 NCERT Solutions - Chapter 3 Trigonometric Function - Exercise 3.1.Augmented Assignment Operators in Python.Class 11 NCERT Solutions - Chapter 7 Permutations And Combinations - Exercise 7.1 This calculator will find the missing variable in the physics equation for Kinetic Energy of a rigid body, when two of the variables are known.Difference Between Mean, Median, and Mode with Examples.What is the Difference between Interactive and Script Mode in Python Programming?.ISRO CS Syllabus for Scientist/Engineer Exam.ISRO CS Original Papers and Official Keys.

GATE CS Original Papers and Official Keys.


 0 kommentar(er)
0 kommentar(er)
